Fractal Generator

The Fractal Generator generates a Mandelbrot fractal.

Since the calculation for each point in the complex plane is independent (ignoring the symmetry about y = 0), the complex plane can be partitioned up into a number of independent sectors and each sector processed in parallel. (Processing each point in parallel would add a large management overhead to the solution.)

The Fractal Generator Application breaks the complex plane into a number of sectors, depending on the number of slaves processors (ie. (n+1)*(n+1), thus 1 slave processor generates 4 jobs, 2 generates 9, etc). As each sector is completed the display is updated. Each slave processor competes for each job, thus faster slaves get more jobs (hence the reason to break the task into more jobs than slaves).

The application automatically detects and re-partitions the complex plane whenever new slaves are added (or removed) from the network. Multi-core slaves are also catered for by both increasing the total number of sectors and allocated more jobs to them.

The GUI can select a sub-section of the complex plane to process, effectively zooming into the data. The maximum zoom is dependent on the numerical precision of the processing.

Fractal Control Dialog

Click to enlarge

Partially Complete Fractal

Enlarge Click to enlarge

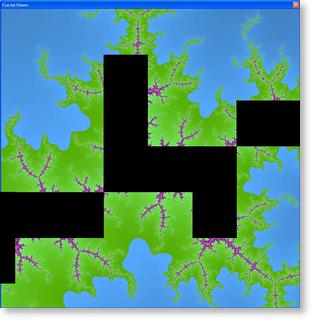
Complete Fractal

Click to enlarge

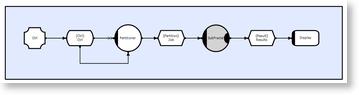
CDL Solution

Click to enlarge

Each time it runs the Partitioner method interrogates the system to identify the number of Slaves (and cores), calculates the number of jobs and opens an appropriate number of connections to the buffered Job store. Each reentrant, slaved SubFractal Method competes for each of the jobs; computes the sub-fractal for the job and writes the results back to the Results store. Each Result is then drawn via the Display Callback.

The two data stores require a Buffer Depth and the Method needs a reentrancy of MAX_NUM_ALLOWABLE_JOBS.

The number of Dims is calculated as the sum of all of the Slave Cores plus 1.

// count num of available CPUs
Uns maxNumSlaves = clp_max_num_slaves();
Uns numDivs = 0;

for ( Uns i = 0; i < maxNumSlaves; ++i )
{
   if ( SlaveConnected( i ) )
   {
      numDivs += ClpSlaveSmpIdx( i );
   }
}
++numDivs;

// subdivide ComplexPlane
Double xRange = MaxX - MinX;
Double yRange = MaxY - MinY;

Double xRes = xRange / X_GRID_SIZE;
Double yRes = yRange / Y_GRID_SIZE;

Uns xSamples = (Uns) ceil( (Float) X_GRID_SIZE / numDivs );
Uns ySamples = (Uns) ceil( (Float) X_GRID_SIZE / numDivs );
Uns xPos     = 0;
Uns yPos     = 0;

Double xFrom = MinX;
Double yFrom = MinY;

// generate jobs
for ( Uns x = 1; x <= numDivs; ++x )
{
   if ( x == numDivs )
     xSamples = X_GRID_SIZE - xPos;

   for ( Uns y = 1; y <= numDivs; ++y )
   {
      if ( y < numDivs )
         CreateJob( xPos, xSamples, xFrom, xRes,
                    yPos, ySamples, yFrom, yRes );
      else
         CreateJob( xPos, xSamples, xFrom, xRes,
                    yPos, (Y_GRID_SIZE - yPos), yFrom, yRes );

      yPos += ySamples;
      yFrom += ySamples*yRes;
   }

   yPos = 0;
   yFrom = MinY;

   xPos += xSamples
   xFrom += xSamples*xRes;
}

The CreateJob() function opens the Partition Store and populates it with the appropriate parameters

void CreateJob( Uns X, Uns SamplesX, Double FromX, Double ResX,
                Uns Y, Uns SamplesY, Double FromY, Double ResY )
{
   this->PartitionTst1Cxn().OpenWrite();
   this->PartitionTst1Rec().Construct();

   this->PartitionTst1Rec().Data().Initialise( X, Y, SamplesX, SamplesY, FromX, FromY, ResX, ResY );

   this->PartitionTst1Cxn().Close();
}

Blueprint Help	Send comments on this topic.
Fractal Generator